|
|
1
30
< Buff行情>
以下代码不起作用,因为某些值超过或超过-1和1(并且不应该是)。有人能指出我做错了什么吗? < /块引用>不,这是对正态分布的标准偏差(构造器中的第二个参数 1 )的误解。
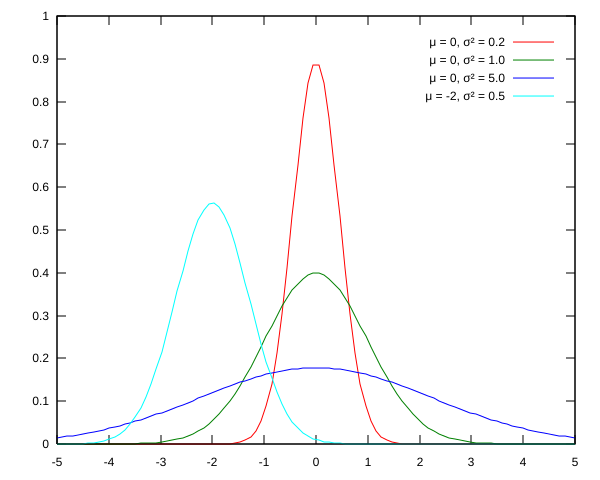
正态分布是常见的钟形曲线。这条曲线有效地告诉你值的分布。接近钟形曲线峰值的值比远离的值(分布的尾部)更可能出现。 标准偏差告诉您值是如何分布的。数值越小,平均值周围的值越集中。数值越大,平均值周围的集中值越小。在下图中,您可以看到红色曲线的方差(方差是标准差的平方)为0.2。将其与平均值相同但方差为1.0的绿色曲线进行比较。可以看到,相对于红色曲线,绿色曲线中的值分布得更广。紫色曲线的方差为5.0,数值分布更广。
因此,这就解释了为什么这些值不局限于
|
|
|
2
8
你没有做错什么。对于正态分布,sigma指定标准 偏差,不是范围。如果你产生足够的样本,你只会看到 其中68%在范围内[平均-西格玛,平均+西格玛],大约95%在2西格玛范围内, 在3西格玛范围内超过99%。 |
|
|
zayd · 在C中Boost程序选项创建的矢量上迭代++ 1 年前 |
|
|
Mimi · CMake使用了错误的boost include目录 1 年前 |
|
|
zxctatar · 如何在一个类中运行两个异步定时器 1 年前 |
|
|
Adrian · 如何确定boost::可选的(和其他)API? 1 年前 |

|
TooTone · boost-pfr是如何获取结构的字段名称的? 1 年前 |