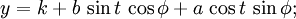如何计算椭圆的轴对齐边界框?

您可以尝试对以任意角度旋转的椭圆使用参数化方程:

x = h + a*cos(t)*cos(phi) - b*sin(t)*sin(phi)  [1]
y = k + b*sin(t)*cos(phi) + a*cos(t)*sin(phi)  [2]

…其中椭圆有中心(H,K)半长轴A和半短轴B,并通过角度phi旋转。

然后,您可以对梯度=0进行区分和求解:

0 = dx/dt = -a*sin(t)*cos(phi) - b*cos(t)*sin(phi)

= & gt;

tan(t) = -b*tan(phi)/a   [3]

它会给你很多关于t的解(其中两个你感兴趣),把它插回到[1]中,得到最大值和最小值x。

重复〔2〕:

0 = dy/dt = b*cos(t)*cos(phi) - a*sin(t)*sin(phi)

= & gt;

tan(t) = b*cot(phi)/a  [4]

让我们尝试一个例子:

考虑(0,0)处的椭圆,a=2,b=1,由pi/4旋转:

〔1〕=gt;

x = 2*cos(t)*cos(PI/4) - sin(t)*sin(PI/4)

〔3〕=gt;

tan(t) = -tan(PI/4)/2 = -1/2

= & gt;

t = -0.4636 + n*PI

我们对t=-0.4636和t=-3.6052感兴趣

所以我们得到:

x = 2*cos(-0.4636)*cos(PI/4) - sin(-0.4636)*sin(PI/4) = 1.5811

和

x = 2*cos(-3.6052)*cos(PI/4) - sin(-3.6052)*sin(PI/4) = -1.5811

我发现了一个简单的公式 http://www.iquilezles.org/www/articles/ellipses/ellipses.htm (忽略Z轴)。

我大致是这样实现的:

num ux = ellipse.r1 * cos(ellipse.phi);
num uy = ellipse.r1 * sin(ellipse.phi);
num vx = ellipse.r2 * cos(ellipse.phi+PI/2);
num vy = ellipse.r2 * sin(ellipse.phi+PI/2);

num bbox_halfwidth = sqrt(ux*ux + vx*vx);
num bbox_halfheight = sqrt(uy*uy + vy*vy); 

Point bbox_ul_corner = new Point(ellipse.center.x - bbox_halfwidth, 
                                 ellipse.center.y - bbox_halfheight);

Point bbox_br_corner = new Point(ellipse.center.x + bbox_halfwidth, 
                                 ellipse.center.y + bbox_halfheight);

这是相对简单,但有点难解释,因为你没有给我们你的椭圆表示方式。有很多方法可以做到。

总之,一般的原理是这样的:不能直接计算轴对齐的边界框。但是,您可以计算X和Y中椭圆的极值作为二维空间中的点。

对于这一点,可以采用方程x(t)=Ellipse_方程(t)和y(t)=Ellipse_方程(t)。求出它的一阶导数,并求出它的根。因为我们要处理的是基于正前方三角法的椭圆。你应该得到一个方程,要么通过atan,acos或asin得到根。

提示:要检查您的代码,请尝试使用未计算的椭圆:您应该在0、pi/2、pi和3*pi/2处得到根。

对每个轴(x和y)都这样做。最多可以得到四个根(如果椭圆退化,例如其中一个半径为零,则更少)。计算根的位置,得到椭圆的所有端点。

现在你就快到了。获取椭圆的边界框就如同扫描这四个点以查找xmin、xmax、ymin和ymax一样简单。

顺便说一句,如果你找不到椭圆方程的话:试着把它简化为一个轴对齐的椭圆,它有一个中心,两个半径和围绕中心的旋转角度。

如果这样做,方程式会变成:

  // the ellipse unrotated:
  temp_x (t) = radius.x * cos(t);
  temp_y (t) = radius.y = sin(t);

  // the ellipse with rotation applied:
  x(t) = temp_x(t) * cos(angle) - temp_y(t) * sin(angle) + center.x;
  y(t) = temp_x(t) * sin(angle) + temp_y(t) * cos(angle) + center.y;

布里安·约翰·尼尔森。 我已经将您的代码转录为c-椭圆角度现在是度数:

private static RectangleF EllipseBoundingBox(int ellipseCenterX, int ellipseCenterY, int ellipseRadiusX, int ellipseRadiusY, double ellipseAngle)
{
    double angle = ellipseAngle * Math.PI / 180;
    double a = ellipseRadiusX * Math.Cos(angle);
    double b = ellipseRadiusY * Math.Sin(angle);
    double c = ellipseRadiusX * Math.Sin(angle);
    double d = ellipseRadiusY * Math.Cos(angle);
    double width = Math.Sqrt(Math.Pow(a, 2) + Math.Pow(b, 2)) * 2;
    double height = Math.Sqrt(Math.Pow(c, 2) + Math.Pow(d, 2)) * 2;
    var x= ellipseCenterX - width * 0.5;
    var y= ellipseCenterY + height * 0.5;
    return new Rectangle((int)x, (int)y, (int)width, (int)height);
}

我认为最有用的公式是这个。从原点的角度phi旋转的省略号有如下公式:

其中(h,k)是中心,a和b是长轴和短轴的大小,t从-pi到pi不等。

由此,您应该能够推导出T dx/dt或dy/dt为0的值。

如果椭圆是由 焦点和偏心距 (对于由轴长度、中心和角度给出的情况,请参见用户1789690的回答)。

也就是说,如果焦点是(x0,y0)和(x1,y1),偏心率是e,那么

bbox_halfwidth  = sqrt(k2*dx2 + (k2-1)*dy2)/2
bbox_halfheight = sqrt((k2-1)*dx2 + k2*dy2)/2

哪里

dx = x1-x0
dy = y1-y0
dx2 = dx*dx
dy2 = dy*dy
k2 = 1.0/(e*e)

我从用户1789690和johan nilsson的答案中推导出公式。

如果你使用OpenCV/C++,并且使用 cv::fitEllipse(..) 函数,可能需要椭圆的边界矩形。在这里,我用迈克的回答提出了一个解决方案:

// tau = 2 * pi, see tau manifest
const double TAU = 2 * std::acos(-1);

cv::Rect calcEllipseBoundingBox(const cv::RotatedRect &anEllipse)
{
    if (std::fmod(std::abs(anEllipse.angle), 90.0) <= 0.01) {
        return anEllipse.boundingRect();
    }

    double phi   = anEllipse.angle * TAU / 360;
    double major = anEllipse.size.width  / 2.0;
    double minor = anEllipse.size.height / 2.0;

    if (minor > major) {
        std::swap(minor, major);
        phi += TAU / 4;
    }

    double cosPhi = std::cos(phi), sinPhi = std::sin(phi);
    double tanPhi = sinPhi / cosPhi;

    double tx = std::atan(-minor * tanPhi / major);
    cv::Vec2d eqx{ major * cosPhi, - minor * sinPhi };
    double x1 = eqx.dot({ std::cos(tx),           std::sin(tx)           });
    double x2 = eqx.dot({ std::cos(tx + TAU / 2), std::sin(tx + TAU / 2) });

    double ty = std::atan(minor / (major * tanPhi));
    cv::Vec2d eqy{ major * sinPhi, minor * cosPhi };
    double y1 = eqy.dot({ std::cos(ty),           std::sin(ty)           });
    double y2 = eqy.dot({ std::cos(ty + TAU / 2), std::sin(ty + TAU / 2) });

    cv::Rect_<float> bb{
        cv::Point2f(std::min(x1, x2), std::min(y1, y2)),
        cv::Point2f(std::max(x1, x2), std::max(y1, y2))
    };

    return bb + anEllipse.center;
}

此代码基于上面提供的代码user1789690,但在Delphi中实现。我已经测试过了,据我所知,它是完美的。我花了一整天的时间寻找一个算法或一些代码,测试了一些不起作用的代码,我很高兴终于找到了上面的代码。我希望有人能发现这个有用。此代码将计算旋转椭圆的边界框。边界框是轴对齐的,不随椭圆旋转。半径是旋转椭圆之前的半径。

type

  TSingleRect = record
    X:      Single;
    Y:      Single;
    Width:  Single;
    Height: Single;
  end;

function GetBoundingBoxForRotatedEllipse(EllipseCenterX, EllipseCenterY, EllipseRadiusX,  EllipseRadiusY, EllipseAngle: Single): TSingleRect;
var
  a: Single;
  b: Single;
  c: Single;
  d: Single;
begin
  a := EllipseRadiusX * Cos(EllipseAngle);
  b := EllipseRadiusY * Sin(EllipseAngle);
  c := EllipseRadiusX * Sin(EllipseAngle);
  d := EllipseRadiusY * Cos(EllipseAngle);
  Result.Width  := Hypot(a, b) * 2;
  Result.Height := Hypot(c, d) * 2;
  Result.X      := EllipseCenterX - Result.Width * 0.5;
  Result.Y      := EllipseCenterY - Result.Height * 0.5;
end;

这是我的函数,用于寻找紧配合矩形到任意方向的椭圆。

我有opencv rect和实现点:

cg-椭圆中心

尺寸-椭圆长轴、短轴

椭圆的角度-方向

cv::Rect ellipse_bounding_box(const cv::Point2f &cg, const cv::Size2f &size, const float angle) {

    float a = size.width / 2;
    float b = size.height / 2;
    cv::Point pts[4];

    float phi = angle * (CV_PI / 180);
    float tan_angle = tan(phi);
    float t = atan((-b*tan_angle) / a);
    float x = cg.x + a*cos(t)*cos(phi) - b*sin(t)*sin(phi);
    float y = cg.y + b*sin(t)*cos(phi) + a*cos(t)*sin(phi);
    pts[0] = cv::Point(cvRound(x), cvRound(y));

    t = atan((b*(1 / tan(phi))) / a);
    x = cg.x + a*cos(t)*cos(phi) - b*sin(t)*sin(phi);
    y = cg.y + b*sin(t)*cos(phi) + a*cos(t)*sin(phi);
    pts[1] = cv::Point(cvRound(x), cvRound(y));

    phi += CV_PI;
    tan_angle = tan(phi);
    t = atan((-b*tan_angle) / a);
    x = cg.x + a*cos(t)*cos(phi) - b*sin(t)*sin(phi);
    y = cg.y + b*sin(t)*cos(phi) + a*cos(t)*sin(phi);
    pts[2] = cv::Point(cvRound(x), cvRound(y));

    t = atan((b*(1 / tan(phi))) / a);
    x = cg.x + a*cos(t)*cos(phi) - b*sin(t)*sin(phi);
    y = cg.y + b*sin(t)*cos(phi) + a*cos(t)*sin(phi);
    pts[3] = cv::Point(cvRound(x), cvRound(y));

    long left = 0xfffffff, top = 0xfffffff, right = 0, bottom = 0;
    for (int i = 0; i < 4; i++) {
        left = left < pts[i].x ? left : pts[i].x;
        top = top < pts[i].y ? top : pts[i].y;
        right = right > pts[i].x ? right : pts[i].x;
        bottom = bottom > pts[i].y ? bottom : pts[i].y;
    }
    cv::Rect fit_rect(left, top, (right - left) + 1, (bottom - top) + 1);
    return fit_rect;
}