代码之家 › 专栏 › 技术社区 › dreeves

从n维单位单纯形均匀随机抽样

wolfram-mathematica random math

dreeves · 技术社区 · 15 年前

从一个n维单位单纯形中随机均匀抽样是一种很好的方法,可以说你想要n个这样的随机数

它们都是非负的,
它们加起来是1,和
n个非负数和1的每个可能向量都是同样可能的。

在n=2的情况下,您希望从位于正象限的直线x+y=1(即y=1-x)的段中均匀采样。在n=3的情况下,从平面x+y+z=1的三角形部分取样,即r3的正八分之一:

(图片来自 http://en.wikipedia.org/wiki/simplex>

注意,选取n个统一的随机数,然后将它们归一化,使之和为1是行不通的。你最终会偏向于不那么极端的数字。

同样,选取n-1均匀随机数,然后取n为1减去n和,也会引入偏差。

wikipedia给出了两种正确执行此操作的算法: http://en.wikipedia.org/wiki/simplex诳random诳sampling (尽管第二个观点目前只声称在实践中是正确的,而不是理论上的。我希望当我更好地理解这一点时,能把它清理干净或澄清。我最初在维基百科的页面上写了一个“警告:这样和这样的论文声称以下内容是错误的”,其他人把它变成了“实践中的作品”警告。)

最后,问题是: 在Mathematica中,您认为单纯形抽样的最佳实现是什么(最好是通过经验证明它是正确的)?

相关问题

5 回复 | 直到 7 年前

Sophie Alpert 15 年前

此代码可以工作:

samples[n_] := Differences[Join[{0}, Sort[RandomReal[Range[0, 1], n - 1]], {1}]]

基本上你只是选择 n - 1 间隔上的位置 [0,1] 把它分开,然后用 Differences .

快速运行 Timing 这表明它比詹纳斯的第一个答案快一点。

brainjam 15 年前

经过一番挖掘,我发现 this page 这给出了Dirichlet分发的一个很好的实现。从那里看来,遵循维基百科的方法1是相当简单的。这似乎是最好的方法。

作为一个测试:

In[14]:= RandomReal[DirichletDistribution[{1,1}],WorkingPrecision->25]
Out[14]= {0.8428995243540368880268079,0.1571004756459631119731921}
In[15]:= Total[%]
Out[15]= 1.000000000000000000000000

100个样品的绘图:

alt text http://www.public.iastate.edu/~zdavkeos/simplex-sample.png

dreeves 15 年前

下面是第二个算法的一个很好的简明实现 Wikipedia :

SimplexSample[n_] := Rest@# - Most@# &[Sort@Join[{0,1}, RandomReal[{0,1}, n-1]]]

这是从这里改编的: http://www.mofeel.net/1164-comp-soft-sys-math-mathematica/14968.aspx (最初它有union而不是sort@join——后者稍快一点。)

(请参阅评论以获取一些证据,证明这是正确的!)

dreeves 15 年前

我是ZDAV的:Dirichlet分布似乎是最简单的方法,ZDAV所指的Dirichlet分布的采样算法也出现在维基百科页面上。 Dirichlet distribution .

在实现方面,首先执行完整的dirichlet分发有点开销,因为您真正需要的是 n 随机的 Gamma[1,1] 样品。比较之下
简单的实现

SimplexSample[n_, opts:OptionsPattern[RandomReal]] :=
  (#/Total[#])& @ RandomReal[GammaDistribution[1,1],n,opts]

完全Dirichlet实现

DirichletDistribution/:Random`DistributionVector[
 DirichletDistribution[alpha_?(VectorQ[#,Positive]&)],n_Integer,prec_?Positive]:=
    Block[{gammas}, gammas = 
        Map[RandomReal[GammaDistribution[#,1],n,WorkingPrecision->prec]&,alpha];
      Transpose[gammas]/Total[gammas]]

SimplexSample2[n_, opts:OptionsPattern[RandomReal]] := 
  (#/Total[#])& @ RandomReal[DirichletDistribution[ConstantArray[1,{n}]],opts]

计时

Timing[Table[SimplexSample[10,WorkingPrecision-> 20],{10000}];]
Timing[Table[SimplexSample2[10,WorkingPrecision-> 20],{10000}];]
Out[159]= {1.30249,Null}
Out[160]= {3.52216,Null}

所以完整的迪里克莱特速度慢了3倍。如果您一次需要1个samplePoints,您可能会通过这样做进一步赢得胜利。 (#/Total[#]&)/@RandomReal[GammaDistribution[1,1],{m,n}] .

Peter O. Manuel Pinto 7 年前

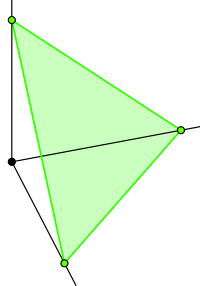
我已经为单纯形上的均匀随机生成创建了一个算法。您可以通过以下链接在本文中找到详细信息: http://www.tandfonline.com/doi/abs/10.1080/03610918.2010.551012#.U5q7inJdVNY

简而言之,可以使用以下递归公式来查找N维单纯形上的随机点:

X _一 = 1 R _一 ^1/n-1

X _K =(1) _i=1 ^K X _我 (1) R _K ^1/N-K ,k=2,…,n-1

X _n =1~ _i=1 ^N-1 X _我

其中r_i是0到1之间的随机数。

现在我正在尝试一种从约束单纯形生成随机均匀样本的算法,即单纯形和凸体的交集。